Interferencia
Interferencia con dos fuentes
Consideremos dos fuentes puntuales separadas cierta distancia, vibrando con la misma frecuencia y amplitud. Las ondas salen en fase de las fuentes y se superponen en todos los puntos del espacio que las rodean generando un patrón de interferencia con máximos y mínimos de intensidad. Podría ser un par de cornetas que emitan ondas sonoras, un par de rendijas angostas que dejen pasar la luz o dos esferas que golpeen la superficie del agua como se muestra en el siguiente video.
A continuación trataremos la superposición de ondas en general en un plano que contiene las fuentes, tal como se ilustra en la siguiente figura.
Sean r1 y r2 las distancias de las fuentes al punto P donde las ondas se superponen. Las ondas salen en fase desde sus respectivas fuentes y dependiendo de la diferencia entre estas dos distancias, llegaran en fase o desfasadas el ángulo φ, una respecto a la otra. Como las ondas vienen descritas por
y1(r1,t)= yo sen(k r1 - ωt)
y
y2(r2,t)= yo sen(k r2 - ωt),
la onda resultante en el punto P es y = y1 + y2. De dónde se obtiene que,
y(r,t) = A sen(k rm - ω t),
con
A = yo cos(π Δr/λ),
rm = (r2+r1)/2,
y
Δr = r2 - r1.
Como la intensidad promedio Io de cada onda es directamente proporcional al cuadrado de su amplitud (yo2), se tiene que la intensidad total I en el punto P es:
I = 4 Io [cos(π Δr/λ)]2.
Por otra parte, si consideramos que
φ1 = arc sen (y/yo1) = k r1 - ω t
y
φ2 = arc sen (y/yo2)= k r2 - ω t;
por lo tanto,
φ = φ2 - φ1 = Δr 2π/λ.
φ = φ2 - φ1 = Δr 2π/λ.
y
Δr π/λ = φ/2.
Así que la ecuación de la intensidad se reduce a:
I = 4 Io [cos( φ/2)]2.
En general, las ondas que llegan al punto P recorren distancias diferentes y debido a esto, puede que lleguen en fase o desfasadas. Se produce la interferencia completamente constructiva sí I = 4 Io ; lo que es equivalente a considerar que cos(φ/2) = 1. Lo cual se cumple cuando:
φ/2 = 0, ±π, ±2π, ±3π, ...
φ/2 = 0, ±π, ±2π, ±3π, ...
En consecuencia,
Δr = a sen θ = 0, λ, 2λ, 3λ,...= m λ, m = 0, ±1, ±2, ±3,...
Es decir, sí:
a sen θ = m λ, m = 0, ±1, ±2, ±3,...
Por otra parte, se da la interferencia completamente destructiva sí I = 0. Lo que es equivalente a considerar que cos(φ/2) = 0; por lo tanto,
φ/2 = ± π/2, ±3π/2, ±5π/2, ...
Finalmente, sí:
a sen θ = (2n -1) λ/2, n = ±1, ±2, ±3,...
En simples palabras: sí la diferencia de caminos recorridos por las dos ondas contiene un número entero (0, λ, 2λ, 3λ,...) de longitudes de onda la interferencia es completamente constructiva, y destructiva sí contiene un número semientero (λ/2, 3λ/2, 5λ/2,...) de longitudes de onda.
El siguiente applet muestra la gráfica de la intensidad I en función de sen θ. Se puede observar que las franjas tienen igual anchura, están igualmente espaciadas, todas alcanzan el mismo valor máximo de intensidad y están comprendida en el rango -1 < sen θ < 1, como es de esperar.
Ver también en: https://www.geogebra.org/material/edit/id/vyp4h8bb
No aparece ningún mínimo. Veamos por qué no. Como a sen θ = λ/2 para n = 1, entonces sen θ = λ/2a = 2. No existe ningún valor de θ que satisfaga esta igualdad. Por consiguiente ni el primer mínimo aparece.
II) Longitud de onda igual a la separación de las fuentes (a = λ)
En el siguiente video, se puede visualizar el patrón de interferencia producido con dos fuentes puntuales (a = 2 λ) que perturban la superficie del agua; se pueden apreciar máximos y mínimos de interferencia en dos y tres dimensiones. Fue realizado con el Applet de Falstad.
En general, por todo lo anterior, podemos concluir que en aquellos puntos de las superficies nodales no se moverán si se trata de ondas en la superficie del agua; tampoco se escuchará sonido alguno si estamos considerando ondas sonoras; y si se trata de ondas luminosas, tales zonas se verán oscuras. Por el contrario, en los puntos de las superficies ventrales se moverán con mayor amplitud, se escucharán sonidos más intensos y las regiones serán más brillantes.
En el caso del experimento Young se utilizan dos rendijas muy angostas, a través de las cuales se hace pasar luz monocromática, es decir de una sola longitud de onda, como se muestra en la siguiente figura.
Cuando las ondas se superponen en la superficie de la pantalla separada la distancia D del sistema de fuentes, produce sobre ésta un patrón de interferencia (luminosa). El patrón de interferencia para este caso y la correspondiente gráfica de la intensidad
El siguiente applet muestra la gráfica de la intensidad I en función de sen θ. Se puede observar que las franjas tienen igual anchura, están igualmente espaciadas, todas alcanzan el mismo valor máximo de intensidad y están comprendida en el rango -1 < sen θ < 1, como es de esperar.
Ver también en: https://www.geogebra.org/material/edit/id/vyp4h8bb
Al variar los valores de a, la separación de las fuentes, y de la longitud de onda λ, cambia el número de franjas (máximos) en el rango indicado. Por ejemplo, al elegir a = 1,5 y λ = 0,5 con los correspondiente deslizadores del applet, se tiene que λ/a = 1/3, y por consiguiente, los máximos de interferencia estarán ubicados en:
sen θ = n λ/a = n/3, para n = 0, ±1, ±2, ±3,...
sen θ = 0, ±1/3, ±2/3 y ±1
y los mínimos en:
sen θ = (n -1) λ/2a = (2n -1)/6, para n = ±1, ±2, ±3,...
sen θ = ±1/6, ±1/2 y ±5/6.
Por supuesto, estos valores coinciden con aquellos de la gráfica del applet.
Discusión de tres casos
En los tres casos siguientes se muestra en la figura superior la interferencia de ondas superficiales en el agua simulada con el applet Falstad (http://www.falstad.com/ripple/); en la figura del medio, la gráfica de la intensidad I en función de θ -no de sen θ-; y debajo, su respectivo diagrama polar (intensidad I en función de la posición angular θ en radianes) a fin de determinar la distribución espacial de la energía:
I) Longitud de onda cuatro veces mayor que la separación de las fuentes (a = λ/4)
Discusión de tres casos
En los tres casos siguientes se muestra en la figura superior la interferencia de ondas superficiales en el agua simulada con el applet Falstad (http://www.falstad.com/ripple/); en la figura del medio, la gráfica de la intensidad I en función de θ -no de sen θ-; y debajo, su respectivo diagrama polar (intensidad I en función de la posición angular θ en radianes) a fin de determinar la distribución espacial de la energía:
I) Longitud de onda cuatro veces mayor que la separación de las fuentes (a = λ/4)
Ondas superficiales en el agua.
Intensidad I en función de θ.
Diagrama polar de la Intensidad I en función de θ.
No aparece ningún mínimo. Veamos por qué no. Como a sen θ = λ/2 para n = 1, entonces sen θ = λ/2a = 2. No existe ningún valor de θ que satisfaga esta igualdad. Por consiguiente ni el primer mínimo aparece.
Ondas superficiales en el agua.
Intensidad I en función de θ.
Diagrama polar de la Intensidad I en función de θ.
Observe la formación de una sola línea nodal en cada cuadrante. Veamos por qué aparece uno solo mínimo. Como a sen θ = (2n -1)λ/2 para n = ±1, entonces sen θ = ± λ/2a = ±1/2. Los valores de θ que satisfacen esta igualdad son: θ = arcsen(1/2) = π/6, 5π/6, 7π/6 y 11 π/6, es decir θ = 30o , 150o , 210o y 330o. Además, para n = ±2 se tiene que a sen θ = ± 2 λ/2 = ±1; pero esta es la condición para los máximos de intensidad (parte superior e interior del diagrama polar, por ejemplo). En resumen, con esta configuración (a = λ) se obtiene sólo un mínimo por cuadrante. Observe también la coincidencia de estos valores con las gráficas I en función θ, tanto en el diagrama polar como en la normal.
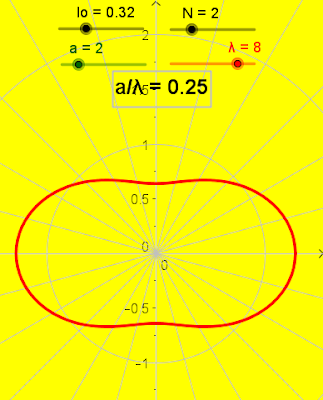
III) Longitud de onda igual a la mitad de la separación de las fuentes (a = 2λ)
Ondas superficiales en el agua.
Intensidad I en función de θ.
Diagrama polar de la Intensidad I en función de θ.
Note la formación de dos línea nodales en cada cuadrante. Se muestra las posiciones de los primeros dos mínimos ubicados en el primer cuadrante en 0,25 rad = 14,5 grados y 0,85 rad = 48,6 grados. Se deja al lector el cálculo restante. Observe también la coincidencia de estos valores con las gráficas I en función θ, tanto en el diagrama polar como en la normal. Se deja al lector el resto del análisis de este caso.
El siguiente applet de
Fernando Martínez ilustra en forma gráfica las zonas de
interferencia constructiva y destructiva. En el caso
particular,
Δr = a sen θ = λ
= constante,
define una hipérbola
cuyos focos son S1 y S2, tal como cualquier curvas verde del diagrama. En cualquier punto de éstas hipérbolas las ondas llegan en fase. Por consiguiente, ésta líneas se conocen como líneas ventrales. Así que, Δr = m λ, m = 0, 1, 2,
3,...define a la familia de hipérbolas donde la interferencia es constructiva. En caso contrario,
cuando
Δr = n λ/2, n = 1, 2, 3,...
se tiene la familia de líneas nodales, donde la interferencia es completamente destructiva.
Δr = n λ/2, n = 1, 2, 3,...
se tiene la familia de líneas nodales, donde la interferencia es completamente destructiva.
En
general, sí las hipérbolas se rotan en el espacio se obtienen superficies
hiperbólicas de revolución que establecen las correspondientes superficies nodales y
ventrales.
Por otra parte, el applet de abajo, muestra el diagrama de interferencia considerando que cada fuente emite ondas circulares cuyos frentes de ondas (circunferencias rojas y azules) se propagan a velocidad constante. Se puede observar que las circunferencias (ondas) se interceptan. En aquellos puntos donde se superponen dos circunferencias del mismo color, la interferencia es constructiva; en caso contrario, donde se interceptan dos de diferente color, la interferencia es destructiva.
Disponible en: https://tube.geogebra.org/student/m103518
Se pueden realizar las siguientes actividades:
1. Elija λ = d = 5. Active el applet pulsando el botón Inicio. Coloque el cursor sobre el punto P (la X) y presiónelo para desplazarlo. Recorra cualquier línea amarilla o verde, y compruebe que λ permanece constante.
2. Cambie de una línea nodal (amarilla) a otra ventral (verde) y compruebe que le corresponden diferentes longitudes de onda.
3. Coloque el cursor en el punto medio entre las dos fuentes. Observe que Δr = 0, así que la interferencia en este punto es constructiva. Considere la línea bisectríz al segmento de recta que une las dos fuentes; sí coloca el cursor sobre cualquier punto de ésta bisectríz podrá comprobar que Δr = 0; de modo que ésta es una línea ventral; además, el plano perpendicular que pase por la bisectríz será un plano ventral donde se dará la interferencia completamente constructiva.
Disponible en: https://tube.geogebra.org/student/m103518
Se pueden realizar las siguientes actividades:
1. Elija λ = d = 5. Active el applet pulsando el botón Inicio. Coloque el cursor sobre el punto P (la X) y presiónelo para desplazarlo. Recorra cualquier línea amarilla o verde, y compruebe que λ permanece constante.
2. Cambie de una línea nodal (amarilla) a otra ventral (verde) y compruebe que le corresponden diferentes longitudes de onda.
3. Coloque el cursor en el punto medio entre las dos fuentes. Observe que Δr = 0, así que la interferencia en este punto es constructiva. Considere la línea bisectríz al segmento de recta que une las dos fuentes; sí coloca el cursor sobre cualquier punto de ésta bisectríz podrá comprobar que Δr = 0; de modo que ésta es una línea ventral; además, el plano perpendicular que pase por la bisectríz será un plano ventral donde se dará la interferencia completamente constructiva.
A fin de calcular como se distribuye la energía, se grafica la intensidad I de las ondas en función de la posición angular θ (radian) con el applet que se muestra abajo. Se puede variar la intensidad Im = 4 Io de las franjas, la separación de las rendijas a y la longitud de onda λ. Se comprueba que, mientras mayor sea el valor de la relación a/λ, el número de franjas de interferencia entre 0 y 2π radianes también sera mayor.
Disponible en: https://tube.geogebra.org/student/m1209821
Disponible en: https://tube.geogebra.org/student/m1209821
ACTIVIDADES:
1. Varíe a o λ de modo que a = λ/4. Compruebe que entre 0 y 2π la curva de interferencia no tiene un mínimo.
2. Varíe a o λ de modo que a = λ y a = 2 λ. Compruebe que entre 0 y 2π la curva de intensidad tiene uno y dos mínimos, respectivamente, tal como se discutió en la sección anterior.
ACTIVIDADES:
1. Varíe a o λ de modo que a = λ/4. Compruebe que entre 0 y 2π la curva de interferencia no tiene un mínimo.
2. Varíe a o λ de modo que a = λ y a = 2 λ. Compruebe que entre 0 y 2π la curva de intensidad tiene uno y dos mínimos, respectivamente, tal como se discutió en la sección anterior.
En el caso del experimento Young se utilizan dos rendijas muy angostas, a través de las cuales se hace pasar luz monocromática, es decir de una sola longitud de onda, como se muestra en la siguiente figura.
I = 4 Io [cos (a π sen θ/λ)]2
se muestra a continuación:
Se puede observar la presencia de una franja brillante central y franjas en ambos lados de ésta, cuyas intensidades van disminuyendo. El applet que toma en cuenta el efecto de la difracción, se mostrará más adelante.
En la presentación siguiente en Power Point, se muestra el procedimiento general para calcular la intensidad I(θ) de las franjas de interferencia mediante el método de los fasores.
Interferencia con tres fuentes
En caso de tres fuentes puntuales
separadas la distancia a, vibrando en fase con la misma frecuencia f y amplitud Ao,
las ondas salen en fase y se superponen en todos los puntos del espacio que las
rodean.
En este caso, para encontrar la intensidad resultante I en el
punto p que dista la distancia r de la fuente central, recurrimos al método de fasores, el cual consiste en representar gráficamente la amplitud de
cada onda como un vector cuya dirección es la diferencia de fase entre cada par
de onda considerada. Así que, Ao representa cada uno de los tres
fasores y φ el desfase entre la onda emitida por la fuente
inferior y la onda emitida por la fuente del medio; las ondas emitidas por la
fuente del medio y la superior también están desfasada en φ; pero
la onda emitida por la fuente inferior está desfasada 2φ respecto a la
superior. Para encontrar la intensidad resultante hay que calcular la suma de
los tres fasores. La construcción que se muestra abajo permite encontrar el
fasor resultante A.
Este es:
A =
2 Ao sen (π/2 - φ) + Ao
A = Ao (1+2 cos φ).
Como Io = c Ao2 (la intensidad
Io es proporcional al cuadrado de la amplitud de la onda ) e I = c A2, entonces I/Io = (A/Ao)2 y por lo tanto:
I = Io (1+2 cos φ)2
donde, φ = 2 π Δr/λ y Δr = a sen θ.
Disponible en: https://tube.geogebra.org/student/m1190872
En el siguiente video, se puede visualizar el patrón de interferencia producido con tres fuentes puntuales que perturban la superficie del agua.
Interferencia con N fuentes
Finalmente se analiza el caso general de la intensidad resultante I producida por N fuentes alineadas con la misma separación a, tal como se muestra en la figura de abajo.
La geometría correspondiente, aplicando el método de fasores, es la que se muestra a continuación. Se puede observar que los fasores individuales están circunscritos en un arco de circunferencia de radio R. Como la figura presenta simetría, se puede dividir en dos partes iguales para simplificar el cálculo del fasor resultante A.
La intensidad I se obtiene como se indica a continuación. De uno de los dos triángulos pequeños del lado izquierdo de la figura se deduce que,
Ao = 2 R sen
φ/2 ,
y del triángulo grande superior que,
A = 2 R sen N φ/2.
Como Io = c Ao2 e I = c A2, entonces I/Io = (A/Ao)2, y por lo tanto:
donde,
φ/2 = a π sen θ / λ.
Esta ecuación de intensidad I(θ) tiene un máximo para Im = N2 Io. Veamos por qué. Para φ/2 = nπ, n = ±1, ±2, ±3,.. se obtiene que sen(Nφ/2)/sen(φ/2) = 0/0; lo cual es una indeterminación, que se resuelve aplicando la regla de L` Hospital. En consecuencia, si
φ/2
= n π , n = ±1, ±2, ±3,..
entonces,
a sen θ = n λ , n = ±1, ±2, ±3,..
Por otra parte, para los mínimos (I = 0) se tiene que
sen (Nφ/2) = 0 ó Nφ/2 = nπ;
Es decir,
a sen θ = nπ/N,
desde n = ±1 hasta ±(N-1); ±(N+1) hasta ±(2N-1); …
(Se
excluyen los valores de n = 0, ±N, ±2N,… porque coincidiría con la ecuación de los mínimos).
El siguiente applet muestra la gráfica de la intensidad I en función de a sen θ.
Disponible en: http://tube.geogebra.org/student/m1232683
ACTIVIDADES:
1.
El applet muestra la gráfica para tres fuentes (N = 3) separadas la misma
distancia (a = 5,4) entre si, emitiendo ondas de una longitud de onda
específica (λ1 = 2). Por
consiguiente este gráfico coincide en forma con el correspondiente del applet
anterior. Observe que entre cada par de máximos principales
consecutivos, se encuentra otro de menor intensidad conocido
como máximo secundario. Al cambiar a N = 2 puede comprobar
que también hay coincidencia con lo mostrado al principio de esta
sección.
2. Sí aumenta N, aparecen varios efectos: i)
se incrementa bastante la intensidad de cada franja de interferencia, porque Imax = N2Io, ii)
el ancho de las franjas disminuyen, y iii) aparecen N-2 máximos secundarios entre los máximos principales.
3. Sí aumenta la separación a entre las fuentes, el ancho de las franjas
disminuye. Para un par de franjas consecutivas como n1 = n y n2 = n+1,
se tiene que a(sen θ2 - sen θ1) = (n2 - n1)λ
= λ. Para valores pequeños de θ, se cumple que (θ2 - θ1) = λ/a, es decir el ancho de las
franjas es Δθ = λ/a. Por consiguiente al aumentar a, disminuye la anchura.
4. Cuando aumenta λ, se incrementa su anchura.
4. Cuando aumenta λ, se incrementa su anchura.
5. Además, si eliges N = 4, λ1 = 3 y a = 3, los máximos y mínimos de interferencia se
pueden ubicar de la siguiente manera:
Máximos:
sen θ = n λ/a = ±1
Mínimos: sen θ = n λ/Na = ±1/4, ±2/4 y ±3/4. Así
que solo hay tres mínimos en las posiciones indicadas aproximadamente. Como sen θ = ±1 es la condición del
máximo, este valor no se puede considerar para el mínimo.
6. Con este applet también se puede simular cómo un haz
de luz blanca se separa en tres de sus colores constituyentes. La longitud de onda del rojo (λ1) es la más larga y
la del azul (λ3) la más corta; el verde (λ2) está comprendida entre estos valores. Si activas las tres longitudes de
onda con las respectivas casillas, aparece el trío de gráficas separadas que se muestra. A medida que el trío se aleja de la franja central, donde todos los colores coinciden, aumentan sus separaciones entre sí, como es de esperar. En el laboratorio se observa que la franja central del patrón de interferencia es blanco, porque en esa región se superponen todos los colores.
El siguiente applet simula el patrón de distribución de la intensidad I de la luz en función de sen θ para -1 < sen θ < 1, para las franjas de interferencia producidas por N rendijas tal como se vería en un experimento de laboratorio. Se puede barrer todo el espectro de luz blanca con un color particular entre 400 nm y 700 nm (1 nm = 10-9 m).
El siguiente applet simula el patrón de distribución de la intensidad I de la luz en función de sen θ para -1 < sen θ < 1, para las franjas de interferencia producidas por N rendijas tal como se vería en un experimento de laboratorio. Se puede barrer todo el espectro de luz blanca con un color particular entre 400 nm y 700 nm (1 nm = 10-9 m).
Disponible en: https://tube.geogebra.org/student/m1278155
ACTIVIDADES:
1. Elija el número de rendijas (N = 3, por ejemplo) y un valor para la separación de las rendijas (a = 2). Pulse el botón de Inicio y observe como se despliega el patrón de intensidades. Dese cuenta que al variar λ, cambia el color de la gráfica y el patrón de franjas. Compruebe la correspondencia existente entre la gráfica y el patrón de franjas.
2. Repita lo anterior para otro valor de N. Observe que al aumentar N, el máximo de intensidad Io se incrementa; disminuya su valor con el deslizador hasta que la gráfica aparezca bien definida en el recuadro.
En esta presentación de Power Point se puede apreciar la deducción paso a paso de la ecuación I(θ) para tres y N fuentes.

















Seria interesante saber calcular la (amplitud) de la onda en una cuerda. Ello es importante para el constructor del cuatro, al calibrar la altura de los trastes a fin de que las cuerdas excitadas no golpeen el diapasón y haya interferencia. También es importante para no calibrar los trastes a una altura mas de la debida, porque ello conlleva a mayor fuerza en la pulsión con los dedos y hace que el ejecutante tenga mayor dificultad para colocar adecuadamente las figuras armonicas. Un calculo adecuado hace que el instrumento suene sin distorsiones y sea m{as suave y plácida la ejecución del instrumento. Especialmente para los principiantes, quienes abandonan el aprendizaje por estas incomodidades y dificultades.
ResponderBorrar