La Luna

Luna Lunera Cascabelera 

La Luna, nuestro único satélite natural, gira alrededor de la Tierra en una órbita elíptica a una distancia media de 384.400 km con una velocidad de 3.700 km/h. Comparada con la Tierra, su diámetro es cuatro veces menor, su masa es 81 veces menor y su gravedad es 6 veces más pequeña. Al girar presenta diferentes aspectos a medida que cambia la superficie iluminada por el Sol, dando lugar a las fases lunares.

Superficie lunar

Su superficie exhibe mares, cráteres, montañas, y valles estrechos y profundos. 

Los mares son grandes extensiones aplanadas rodeadas de montañas, con muchos cráteres y atravesados por pronunciados riscos; en particular el Océano de las Tormentas con forma poligonal, de más o menos 1.800 km de diámetro, es el más grande, y se cree que se formó con el magma que brotó desde sus profundidades. Otros mares posiblemente se formaron cuando el magma rellenó las cavidades dejadas por los choques de grandes asteroides contra la superficie lunar. Los mares estás rodeados de montañas de hasta 9.100 metros. 

Los cráteres, formados por impactos de meteoritos, son estructuras planas de forma circular con un pico central, algunos de los cuales tienen hasta 4 km de alto; sus diámetros varían desde algunos centímetros hasta 260 km. 

Tiene también más de mil profundos valles con extensiones que llegan a 500 km de longitud.

Movimientos y consecuencias

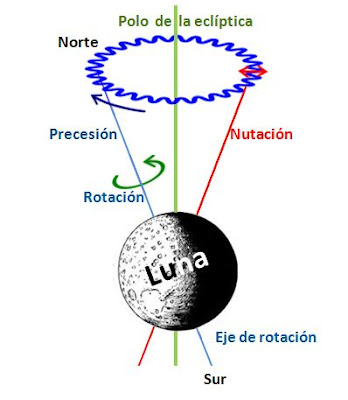
Al igual que el trompo cuando baila, la Luna tiene cuatro movimientos: Traslación (revolución sideral) alrededor de la Tierra en una órbita elíptica en un tiempo de 27 d 7 h 43 m 11 s; rotación sobre su propio eje con el mismo periodo del movimiento anterior; precesión de su eje, el cual se encuentra a 83o 20m respecto al plano de la órbita de la Tierra en un tiempo de 18,6 años y nutación o cabeceo del eje de rotación en un tiempo de 173 días. 

Como consecuencias de estos movimientos, la Luna se nos presentan con diferentes facetas, como las siguientes. Su rotación, así como la rotación y traslación de la Tierra, hace que cada día nuestro satélite retrase 51 minutos más su salida por el este. Presenta fases lunares (cambios de luminosidad) durante cada intervalo de tiempo de 29 d 12 h 44 m 3 s (revolución sinódica). Siempre vemos la misma cara porque su periodo de rotación sobre su eje es igual al periodo de traslación alrededor de la Tierra. Sin embargo, por efecto de la inclinación de su eje de rotación se produce la libración (balanceo) en latitud (de norte a sur); y debido a la excentricidad de su órbita -anda más rápido en el perigeo (punto más cercano a la Tierra) que en el apogeo (punto más alejado de la Tierra)- se produce la libración en longitud (de este a oeste). Estos balanceos en latitud y longitud, permite observar una décima de la superficie de su hemisferio oculto. La excentricidad de su órbita elíptica hace que se vea más grande en el perigeo que en el apogeo. El movimiento de traslación junto a la gravedad activan las mareas.

Superficie lunar

Su superficie exhibe mares, cráteres, montañas, y valles estrechos y profundos.

Los mares son grandes extensiones aplanadas rodeadas de montañas, con muchos cráteres y atravesados por pronunciados riscos; en particular el Océano de las Tormentas con forma poligonal, de más o menos 1.800 km de diámetro, es el más grande, y se cree que se formó con el magma que brotó desde sus profundidades. Otros mares posiblemente se formaron cuando el magma rellenó las cavidades dejadas por los choques de grandes asteroides contra la superficie lunar. Los mares estás rodeados de montañas de hasta 9.100 metros.

Los cráteres, formados por impactos de meteoritos, son estructuras planas de forma circular con un pico central, algunos de los cuales tienen hasta 4 km de alto; sus diámetros varían desde algunos centímetros hasta 260 km.

Tiene también más de mil profundos valles con extensiones que llegan a 500 km de longitud.

Origen

La hipótesis general aceptada hoy en día es que el sistema Tierra-Luna se formó por la colisión de un cuerpo celeste del tamaño del planeta Marte con la joven Tierra. Parte del material dispersado se puso en órbita alrededor de ésta y se fue fusionando poco a poco hasta formar nuestro satélite.

El juego del escondite

Nuestra luna presenta diferentes zonas luminosas de su superficie, a medida que se traslada alrededor de la Tierra, en su revolución sinódica de 29 d 12 h 44 m 3 s. Podemos apreciar su esplendor por el reflejo de una pequeña cantidad de la luz solar que la baña. Cuando no la podemos ver es porque se encuentra en dirección al Sol y lo más cerca de éste; en esta posición, cuando la luz sólo ilumina el hemisferio posterior que nunca vemos, se encuentra en fase de Luna Nueva o Novilunio. A medida que la Luna avanza se va iluminando poco a poco la cara frente a la Tierra, hasta que transcurrido siete días entra en fase de Cuarto Creciente, cuando sólo la mitad del disco se ve brillante. En la posición contraria, alejada del Sol, su disco se ve completamente iluminado durante el ocaso; es la fase de Luna Llena o Plenilunio, que ocurre 14 días después y hace su salida por el horizonte a las 6.00 pm. Finalmente, cuando la Luna sigue avanzando, después de 21 días, el área iluminada va disminuyendo hasta mostrar sólo la mitad brillante; se encuentra en la fase de Cuarto Menguante.

ASTRONOMÍA Y ASTROFÍSICA

QUIBARIO

Revista de divulgación 
del 
Centro de 
Investigaciones de Astronomía
 CIDA

Asesor del tema científico:
Orlando B. Escalona T.

SIGUE...

XIX Encuentro con la Física

                                                                         XIX

                                       Encuentro con la Física, Química,                                                  Matemática  y  Biología

Amigos todos:

Durante 18 años, a pesar de tantas dificultades, hemos llevado a cabo esta hermosa actividad.

Este año estamos a la saga de cristalizar su decimonovena edición. El XIX Encuentro con la Física, Química, Matemática y Biología, se llevará a cabo del 04 al 06 de noviembre, 2019, en la Facultad de Ciencias de la Ilustre Universidad de Los Andes, en Mérida, Venezuela!

Todos los niños y jóvenes, maestros, profesores, padres y representantes, están cordialmente invitados a disfrutar de unas jornadas hermosas, donde la ciencia es la protagonista.

Como siempre, la entrada es completamente gratuita.

Nuestros profesores y estudiantes universitarios han preparado lindos y divertidos experimentos.

Los esperamos!!!!

Con afecto,
Patricia Rosenzweig

XXIII Escuela Venezolana para la Enseñanza de la Matemática

XXIII 

Escuela Venezolana para la Enseñanza

 de la 

Matemática

Cuentos de la Vía Férrea

Cuentos

de la

 Vía Férrea



Disponible también en: http://senderospedagogicos.blogspot.com/p/nuestra.html

Paradoja de la copa de martini

LA PARADOJA 

DE LA 

COPA DE MARTINI

Figura 1. Copa de coctel para servir el martini.

La copa para servir el Martini tiene forma cónica. Si se llena hasta el nivel que muestra la figura 1, da la impresión de que tal volumen de líquido no fuera exactamente la mitad de su capacidad, sino mucho mas. He ahí la paradoja. En el siguiente video se aprecia lo anterior.

     

Video 1. Paradoja de las copas. 

Disponible en: https://www.youtube.com/watch?v=-esV5exS6R4

Figura 2. Dibujo de la copa en un plano paralelo al eje, con los respectivos parámetros para la elaboración del modelo.  Tomado de Naukas.

Figura 3. Dibujo de la copa con otros parámetros adicionales para abordar 

la elaboración del modelo.

La presente paradoja se describe en la página web Naukas. En la misma se hace una presentación detallada de la paradoja. Por su parte, también Retos de Matemática, Física, Química y otras Ciencias retoma el problema de la copa y lo presenta como uno de sus desafios con el siguiente enunciado:

"¿Hasta qué altura x tendré que llenar esta copa para que dentro haya justamente la mitad del volumen total?" 

De esta última lectura surgió nuestra motivación para presentar la solución de este problema desde otra perspectiva. 

Solución: Supongamos que la copa es cónica, tiene las dimensiones que se indican en la figura y que su fondo es plano. Esto significa que el interior de la copa tiene un volumen que se corresponde con el volumen de un cono truncado. Sea v el pequeño volumen de vidrio del vértice de la copa en su parte inferior. Sea V el volumen que tendría la copa, si fuera un cono perfecto; como no lo es, cuando está vacía su volumen es V-v. De igual forma, V* sería el volumen de vino si la copa fuera un cono perfecto; en consecuencia el volumen de vino es V*- v . De acuerdo al enunciado, entonces V - v = 2 (V*- v). Como el volumen de los conos anteriores son V = π r² H/3, V* = π r*² x/3  y  v =  π b² a/3, donde a es la altura del cono ubicado en el vértice y b el radio de su base, se tiene que

π r² (H+a)/3 – v = 2 π  (x+a)² tg²α (x+a)/3 - 2 v,

donde tg α = b/a= r/(H+a) y a = r/tg α – H.

Al despejar x de la ecuación se obtiene que

x = {(r² (H+a) – v)/2tg²α }^1/3 – a.

Simplificando un poco, se tiene finalmente que:

x = {(H+a)³/2 – π a³/6}^1/3 – a.

En esta ecuación no aparece r, lo que significa que la profundidad x del agua es independiente de la abertura de la boca de la copa expresada mediante su radio.

El caso particular tratado por Naukas* se obtiene cuando a « H. Por consiguiente  

x ≈ H/2^1/3.

En la figura 4 se muestra la representación gráfica de la ecuación anterior y la simulación del nivel del liquido en la copa cuando se cumple la relación establecida entre los volúmenes. La misma fue realizada con un applet de Geogebra.

Figura 4. Representación gráfica de la profundidad x del martini en función de la profundidad H de la copa cónica para b = 0 ( recta azul) y la copa de fondo plano para b > 0 (curva roja); x y H se miden en unidades arbitrarias. Ver en: https://www.geogebra.org/m/uyku5deb

Se discuten dos casos: 

1) Copa cónica con fondo puntiagudo (b = 0). La recta azul describe en este caso límite, cómo se comporta la profundidad x del líquido en función del tamaño H de la copa.  Observe que el nivel del líquido en la copa ocurre para x = 0.8 H, cuando la profundidad de la copa es de 1. Para otra copa mas pequeña cuyo valor sea H = 0,60,  por ejemplo, entonces x = 0,48, como se puede constatar con la recta azul. A la derecha se muestra en una representación gráfica de la copa, el nivel del líquido mediante el segmento de recta azul que se acciona con el deslizador x, ubicado arriba a la derecha del applet. Observe que si H = 1, entonces x = 0,8 H.

2) Copa cónica con fondo plano (b > 0). La curva roja considera la dependencia de x con H. Para un valor pequeño de b comparado con H, la curva tiende a la forma linear y se comporta según el trozo de recta de la parte superior; a medida que b es comparable a H, la descripción de x(H) depende de la parte inferior de la curva. Los valores negativos de x no tienen significado físico.    

Observe también que en la representación gráfica de la derecha, el área que representa al líquido es mayor que el área vacía de la copa. Dejamos al lector acucioso demostrar que el área del líquido es 1/2^2/3 (0,62) veces mayor que el área vacía. En consecuencia, la impresión que la imagen de la copa produce en la retina es que el volumen de la parte inferior (con martini) es mayor que el volumen de la parte superior (sin martini). Este hecho explica la jugada de nuestro sentido común.  
  

Referencias

1. Miguel Artime M. et al. (2015). Naukas: Recuperado de: https://naukas.com/2014/03/24/la-paradoja-de-la-copa-de-martini/

2. Gonzàles R., May. (2018). Retos de Matemática, Física, Química y otras Ciencias. Recuperado de: https://www.facebook.com/groups/794248687378973/

XXII Escuela Venezolana

 para la 

Enseñanza de la Matemática 2018

Información: 

Tlf. y Fax: 
(0274) 240.13.45
(0416) 6152.810 / (0414) 8136.897

e-mail: 
aristide@ula.ve

Horario de Atención: 
9 a 12am de Lunes a Viernes.  

Más información en:

 http://evem-merida.blogspot.com/p/cursos.htmlhttp://evem-merida.blogspot.com/p/cursos.html

Santa Bárbara del Zulia-Venezuela

Hacia la nueva Ciudad 

Puerto Sur del Lago
Autor: el Poeta Alexis Fernández

En el imaginario colectivo surlaguense, la navegación en piraguas y vapores es uno de los referentes simbólicos más recurrentes. A finales del siglo XIX y en las primeras seis décadas del siglo XX, la piragua se convirtió en un medio de transporte de carga y pasajeros, no sólo eficaz sino sumamente atractivo al comercio establecido entre las poblaciones del sur del Lago, norte santanderiano y el Puerto de Maracaibo.

Origen de la palabra piragua 

   

Documental "Metáforas del Agua" del poeta y escritor zuliano Alexis Fernández, y dirigido por Patricia Ortega. El tema musical fue compuesto por el trovador venezolano Israel Colina.

Disponible en: https://www.youtube.com/watch?v=qtO2D-zjVx8

 A ese tronco ahuecado lanzado al agua como embarcación, los antiguos caribes lo llamaron piragua. “Usan estas canoas tan grandes o mayores como lo que he dicho, e llámanlas los caribes piraguas” nos recuerda en su Glosario de voces indígenas, el maestro Lisandro Alvarado. Toscas pero útiles como precisas tablas y rústicos instrumentos emplearon en su avezada construcción que permitieron a los intrépidos navegantes acercarse a las colonias holandesas y a Las Antillas. En esas mismas embarcaciones los grupos amerindios se desplazaron por la cuenca del lago Coquivacoa, en una incesante dinámica de intercambios, encuentros y desencuentros.

Las piraguas esos troncos de madera lanzados al agua

La piragua es un tronco de madera lanzado al agua, me cuenta Arcángel Muñoz, patrón de piragua, quien lleva más de cuarenta años bregando en estas aguas. Tallada a pulso de hacha y escoplos, con la madera más recia que nace en estas mismas tierras, se construyeron las embarcaciones que durante años surcaron las aguas de los ríos del sur hacia el lago de Maracaibo y del puerto de Maracaibo a los recónditos malecones del sur. Más de un centenar de piraguas avecindaron las cosechas de las laderas de las montañas, los productos del agro surlaguense, la floreciente pescadería y un efectivo movimiento de pasajeros al puerto de Maracaibo, en un incesante intercambio de navegación de cabotaje que incluía los puertos de Encontrados, Santa Bárbara y Santa Cruz de Zulia, Bobures, Gibraltar, Moporo y La Ceiba, hasta mediados de los años 1964 del pasado siglo. Las rutas ferrocarrileras cumplían su cometido de acercar a sus malecones dichos productos. Esta de las últimas que quedan, quizás la última (y ello es realmente grave en cuanto enseña del pasado histórico reciente) emblemáticamente llamada La Merideña, es ese vestigio de casa de madera lanzada al agua.

Simulación del yoyo

Simulación de la cinemática del yoyo

con GeoGebra

El yoyo o yoyó es uno de los juguetes de mayor popularidad a nivel mundial. Se cree que fue inventado en tiempos de la China milenaria. La figura de arriba, reporte de excavaciones arqueológicas, establece la evidencia de que hace 2.500 años también formó parte del entretenimiento del pueblo griego.

Es interesante estudiar su física. Con él se puede enseñar la transformación de la energía potencial en cinética y viceversa, así como conceptos propios de cuerpos rígidos en movimientos: momento de inercia y torque, velocidad angular, cantidad de movimiento angular, entre otros.

Vectores y sus Aplicaciones

¡Este material se encuentra en etapa de  redacción!

Introducción

El presente material didáctico fue escrito para los participantes del curso Vectores y sus Aplicaciones de la XXI Escuela Venezolana de Enseñanza de la Matemática que tuvo lugar del 10 al 15 de septiembre de 2017 en los espacios académicos de la Facultad de Ciencia de la Universidad de Los Andes, Mérida, Venezuela. 

Aunque el curso se desarrolló sin la rigurosidad exigida por el pensum de cualquier licenciatura formal en matemática, sí se hizo hincapié en la utilización de herramientas de las Tics para facilitar el proceso de su enseñanza y aprendizaje. Se dejaron de lado las precisas y contundente demostraciones del curso tradicional de álgebra vectorial, por el diseño de estrategias digitales para la representación vectorial en el espacio euclidiano mediante applets elaborados con GeoGebra; software matemático de libre uso, escrito en Java para múltiples plataformas, el cual consiste de un procesador interactivo, que conjuga geometría, algebra y cálculo, y permite el trazado dinámico de construcciones geométricas, representaciones gráficas, tratamiento algebraico y cálculo de funciones reales, sus derivadas e integrales. En realidad, la discusión se orientó más hacia la didáctica de las matemáticas, que a los profundos temas del mundo vectorial, sin caer en la inútil e innecesaria simplicidad. Por supuesto, trató de suma y resta de vectores, y multiplicación escalar y vectorial de vectores, con algunos ejemplos de aplicaciones en física e ingeniería. Así que, se insistió en el diseño y uso de applets para una clase novedosa de vectores. Lo que permitió contrastar los resultados de la representación gráfica con los obtenidos mediante los algoritmos matemáticos.

Más en: http://senderospedagogicos.blogspot.com/p/blog-page_69.html

Determinación de g

Experimento Virtual 
3
Determinación de 

g

mediante caída libre

Mediante dos applets se determina la aceleración de la gravedad g en dos ambientes gravitacionales semejantes: la Tierra y la Luna. Se discuten las características del movimiento rectilíneo uniformemente acelerado (MRUA) de objetos cayendo en sus campos gravitacionales, y se comparan sus efectos. El texto donde se describe el experimento y el procedimiento a seguir, se encuentra alojado en Yumpu. Se despliega haciendo click abajo.

MRU

Experimento Virtual 

1

Movimiento Rectilíneo Uniforme (MRU)

Recientes avances en pedagogía y tecnología plantean un importante reto al docente de física. Nuevos instrumentos tecnológicos están a su disposición, que le permiten analizar la diversidad de procesos naturales de manera efectiva, presentar sus conceptos, formular sus leyes, y realizar aplicaciones. Uno de estos recursos didácticos lo representan las simulaciones; las cuales no sólo están en manos del científico para su trabajo especializado, sino que ahora se encuentran a disposición libre de docentes y estudiantes para la comprensión de su entorno físico cotidiano.

Diferentes tipos de software se han creado para simular procesos naturales; uno de gran utilidad, disponibilidad y de uso extendido a nivel mundial es GeoGebra, especialmente diseñado para elaborar applets de matemática, y que perfectamente se puede usar en enseñanza y aprendizaje de la ciencia, y en particular de la física. GeoGebra es un software matemático interactivo de libre uso, escrito en Java para múltiples plataformas por su creador Markus Hohenwarter (2001, en la Universidad de Salzburgo). Básicamente es un procesador interactivo geométrico y algebraico, que conjuga geometría, algebra y cálculo. Es decir, GeoGebra permite el trazado dinámico de construcciones geométricas, representaciones gráficas, el tratamiento algebraico y el cálculo de funciones reales, sus derivadas e integrales.

Aprovechando estos recursos de la Web, y bajo la perspectiva de que existen formas alternativas de aprender y enseñar física, es que se ha elaborado este trabajo, con la pretensión de que sea un "libro virtual" de utilidad pedagógica. 

Con esto experimentos virtuales se presentan y analizan los conceptos más relevantes del movimiento rectilíneo uniforme (MRU) y uniformemente acelerado (MRUA). 

Con este estrategia didáctica no se pretende sobreponer la simulación del fenómeno físico a la demostración experimental directamente en el aula o el laboratorio; al contrario, se busca conjugar ambos recursos para lograr las competencias requerida en la enseñanza de la física.

Las simulaciones se encuentran alojadas en la página oficial de GeoGebra (https://tube.geogebra.org/). 

El texto donde se describe el experimento y el procedimiento a seguir, se encuentra alojado en la aplicación on-line Yumpu como libro de texto digital. Se despliega haciendo click en  "Mecánica. Movimiento Rectilíneo Uniforme". Se agradece la participación activa de Emily G. Escalona C. en la utilización del applet y la elaboración de las gráficas que se muestra.

https://www.yumpu.com/es/document/view/58508150/movimiento-rectilineo-uniforme-mru

También se encuentra disponible en formato digital en este mismo blog en la sección de Nuestras Publicaciones. 

Con este applet se simulan los experimentos virtuales. Pulse sobre la imagen o en la dirección URL para activarlo desde la plataforma de GeoGebra.

Disponible en: https://www.geogebra.org/m/ZPVjGHEj

MRUA

Experimento Virtual
2

Movimiento Rectilíneo Uniformemente
Acelerado

Recientes avances en pedagogía y tecnología plantean un importante reto al docente de física. Nuevos instrumentos tecnológicos están a su disposición, que le permiten analizar la diversidad de procesos naturales de manera efectiva, presentar sus conceptos, formular sus leyes, y realizar aplicaciones. Uno de estos recursos didácticos lo representan las simulaciones; las cuales no sólo están en manos del científico para su trabajo especializado, sino que ahora se encuentran a disposición libre de docentes y estudiantes para la comprensión de su entorno físico cotidiano.

Diferentes tipos de software se han creado para simular procesos naturales; uno de gran utilidad, disponibilidad y de uso extendido a nivel mundial es GeoGebra, especialmente diseñado para elaborar applets de matemática, y que perfectamente se puede usar en enseñanza y aprendizaje de la ciencia, y en particular de la física. GeoGebra es un software matemático interactivo de libre uso, escrito en Java para múltiples plataformas por su creador Markus Hohenwarter (2001, en la Universidad de Salzburgo). Básicamente es un procesador interactivo geométrico y algebraico, que conjuga geometría, algebra y cálculo. Es decir, GeoGebra permite el trazado dinámico de construcciones geométricas, representaciones gráficas, el tratamiento algebraico y el cálculo de funciones reales, sus derivadas e integrales.

Aprovechando estos recursos de la Web, y bajo la perspectiva de que existen formas alternativas de aprender y enseñar física, es que se ha elaborado este trabajo, con la pretensión de que sea un "libro virtual" de utilidad pedagógica.

Con este experimento virtual se presentan y analizan los conceptos más relevantes del movimiento rectilíneo uniforme (MRU) y uniformemente acelerado (MRUA).

Con este estrategia didáctica no se pretende sobreponer la simulación del fenómeno físico a la demostración experimental directamente en el aula o el laboratorio; al contrario, se busca conjugar ambos recursos para lograr las competencias requerida en la enseñanza la física. 

    El texto donde se describe el experimento y el procedimiento a seguir, se encuentra alojado en Yumpu. Se despliega haciendo click abajo. Se agradece la participación activa de Emily G. Escalona C. en la utilización del applet y la elaboración de las gráficas que se muestran. 

Faraday

Reseña 

de 

Libros Viejos de Física

Curso de

Seis conferencias sobre las diversas fuerzas de la materia, y sus relaciones entre sí

(Course of six lectures on the various forces of matter, and their relations to each other)

Michael Faraday  

Este libro de Faraday (1791-1867), físico y químico inglés, contiene la transcripción de seis de sus magistrales conferencias sobre Física y Química. Estaban dirigidas a mentes jóvenes deseosas de estar al día con el conocimiento científico de su época. Se puede leer en inglés en el sitio Internet Archive, "una biblioteca sin fines de lucro de millones de libros gratis, películas, música, software, sitios web, y mucho más".

Texto original

Internet Archi

 

Revista Ciencia Cotidiana

Revista

Ciencia Cotidiana

Autores: 

Orlando B. Escalona T.

Gregoria Cabral

Ciencia Cotidiana

Open publication - Free publishing

Física Cotidiana 2

Física Cotidiana
La Cocina

Se propone abordar la enseñanza de la ciencia a partir de la cotidianidad. Los fenómenos naturales que transcurren diariamente en nuestro ámbito espacio-temporal cotidiano los convierten en simples hechos comunes y de aparente simplicidad; sin embargo, en todo momento y alrededor nuestro, se producen cambios de diferente naturaleza que inciden de una u otra manera en el desenvolvimiento de nuestras vidas. Ignorarlos sólo contribuye a acentuar el desconocimiento de nuestra realidad objetiva; prestarles atención, motiva el análisis y la reflexión y nos prepara para desentrañar los “secretos” del mundo natural. Aunque lo cotidiano está sujeto al contexto sociocultural, económico, político y religioso de los individuos, existe sin embargo, un conjunto de objetos, conceptos y procesos naturales que son comunes para todo el mundo, independientemente del lugar donde se encuentren. Por supuesto, la ocurrencia cotidiana para el niño warao es muy diferente a la del niño de Curarigua, y más aún, a la del niño de un rascacielos típico de cualquier urbe norteamericana. No obstante, por ejemplo, el aire y el agua con toda la serie de procesos físicos, químicos y bioquímicos que conllevan su consumo, son cotidianos para todos los seres humanos; así como el fuego con los conceptos de energía, calor, propagación, temperatura; igualmente la gravedad con el conjunto de procesos mecánicos que la involucran; el día y la noche con los procesos astronómicos observables desde cualquier parte del planeta.

     Por otra parte, es indiscutible que entre los ambientes más cotidianos, se cuenta la cocina con todos sus enseres y procesos físicos, químicos, fisicoquímicos, entre otros; igualmente, el ámbito de la habitación con la parafernalia de artículos de tocador, vestidor y la cama. Además, hay que agregar las actividades lúdicas cotidianas propias de los juegos y juguetes; así como el ambiente inmediato externo al hogar y la escuela, el planeta Tierra y el Universo.

 

Física Cotidiana 1

Física Cotidiana
Entretenimiento y Actividad Lúdica

Los humanos, nos diferenciamos de las demás especies del planeta por nuestra capacidad creativa de modificar y adaptar el entorno a las necesidades inmediatas. Con las múltiples inteligencias que nos caracteriza, como indica H. Gardner, se han resuelto los problemas más intrincados desde los tiempos remotos y se han elaborado todo tipos de productos, desde los más sencillos hasta los más sofisticados e inverosímiles. Entre estos, destacan los juguetes, presentes en todas las culturas del mundo desde los tiempos primitivos, vitales para la socialización de los seres humanos, algunos de los cuales han generado esquemas de comportamiento colectivos. Existe diversidad de juegos y juguetes tradicionales propios de cada cultura, pero también destacan aquellos que se han convertidos en universales y que forman parte del acervo cultural mundial. 

     En la actualidad, el juguete se usa no sólo para el entretenimiento y la diversión de grandes y pequeños, sino también para la adquisición de conocimiento científico en los cursos de ciencias puras y aplicadas, así como para el desarrollo de habilidades y destrezas contempladas en cada una de las inteligencias múltiples de manejo obligado por cualquier docente en las instituciones educativas, a saber: lógica matemática, lingüística, espacial, físico-cinestésica, musical, interpersonal, intrapersonal y naturalista.